문제
최근에 ICPC 탐사대는 남아메리카의 잉카 제국이 놀라운 문명을 지닌 카잉 제국을 토대로 하여 세워졌다는 사실을 발견했다. 카잉 제국의 백성들은 특이한 달력을 사용한 것으로 알려져 있다. 그들은 M과 N보다 작거나 같은 두 개의 자연수 x, y를 가지고 각 년도를 <x:y>와 같은 형식으로 표현하였다. 그들은 이 세상의 시초에 해당하는 첫 번째 해를 <1:1>로 표현하고, 두 번째 해를 <2:2>로 표현하였다. <x:y>의 다음 해를 표현한 것을 <x':y'>이라고 하자. 만일 x < M 이면 x' = x + 1이고, 그렇지 않으면 x' = 1이다. 같은 방식으로 만일 y < N이면 y' = y + 1이고, 그렇지 않으면 y' = 1이다. <M:N>은 그들 달력의 마지막 해로서, 이 해에 세상의 종말이 도래한다는 예언이 전해 온다.
예를 들어, M = 10 이고 N = 12라고 하자. 첫 번째 해는 <1:1>로 표현되고, 11번째 해는 <1:11>로 표현된다. <3:1>은 13번째 해를 나타내고, <10:12>는 마지막인 60번째 해를 나타낸다.
네 개의 정수 M, N, x와 y가 주어질 때, <M:N>이 카잉 달력의 마지막 해라고 하면 <x:y>는 몇 번째 해를 나타내는지 구하는 프로그램을 작성하라.
입력
입력 데이터는 표준 입력을 사용한다. 입력은 T개의 테스트 데이터로 구성된다. 입력의 첫 번째 줄에는 입력 데이터의 수를 나타내는 정수 T가 주어진다. 각 테스트 데이터는 한 줄로 구성된다. 각 줄에는 네 개의 정수 M, N, x와 y가 주어진다. (1 ≤ M, N ≤ 40,000, 1 ≤ x ≤ M, 1 ≤ y ≤ N) 여기서 <M:N>은 카잉 달력의 마지막 해를 나타낸다.
출력
출력은 표준 출력을 사용한다. 각 테스트 데이터에 대해, 정수 k를 한 줄에 출력한다. 여기서 k는 <x:y>가 k번째 해를 나타내는 것을 의미한다. 만일 <x:y>에 의해 표현되는 해가 없다면, 즉, <x:y>가 유효하지 않은 표현이면, -1을 출력한다.
문제 풀이
문제 접근
카잉 달력 문제는 통상적으로 중국인의 나머지 정리(Chinese Remainder Theorem, CRT) 형태로 풀이하는 것이 유명하다.
문제를 간단히 바꾸면 “다음 식을 만족하는 T를 찾는 것”과 같다.
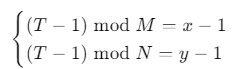
이를 일반화해서 구현하는 방법은 다음과 같다.
- 연도 T를 x로 시작해서, M씩 증가시키면서
- (T−1)mod N+1이 y와 같은지 검사
- 만약 검사 범위 T≤M×N를 넘어가면 답이 없으므로 -1 (왜 M*N이 검사 범위인지는 마지막에 설명)
왜 이런 식으로 하냐면,
- (T−1) M+1=x이면 (T−1)≡(x−1)(modM), 즉 T≡x(modM)
그렇다면 T가 x, x + M, x + 2M, ... 형태로 나열될 것이고, 그 중에서 (T−1) N+1=y를 만족하는지 찾으면 된다.
문제 해결
import sys
A=int(sys.stdin.readline())
for i in range(A):
M,N,x,y=list(map(int,sys.stdin.readline().split()))
limit=M*N
candidate=x
answer=-1
while candidate<=limit:
if (candidate-y)%N==0:
answer=candidate
break
else:
candidate+=M
print(answer)
왜 limit가 M×N일까?
왜 M×N이 상한(최대 해)인가?
- 카잉 달력의 구조
- 각 해는 (T−1) M+1과 (T−1) N+1의 형태로 표시된다.
- 연도 T가 1씩 증가할 때마다, 앞의 식들은 주기적으로 반복된다.
- <1:1>부터 <M:N>까지의 ‘주기’
- 문제에서 “카잉 달력은 <1:1>에서 시작해서 매년 x는 1부터 M까지, y는 1부터 N까지 돌아가며 증가한다”고 했다.
- ‘<M:N>이 마지막 해다’라는 것은, (문제에서 주어진 설정상) 이 이후로 달력이 더 이상 가지 않는다 혹은 새로운 사이클로 넘어가기 전까지의 최대 해라는 의미로 볼 수 있다.
- 만약 우리가 1년 차부터 차례대로 모든 해를 표현해 보면, 최대한 길게 가도 M×N번을 넘으면 ‘다시 초기처럼 반복되는 사이클’로 간주할 수 있다.
- 실제로는 LCM(M,N)(최소공배수)이 주기가 될 수도 있지만, 문제에서 “<M:N>이 마지막 해”라고 정의해 버렸으므로, 이를 포함하는 최댓값으로 M×N을 잡아도 충분하다.
- M과 N이 서로소일 때는 LCM(M,N)=M×N이 되고, 서로소가 아닐 때도 M×N은 LCM(M,N)보다 크거나 같은 상한이 된다.
- 코딩 시의 편의
- 우리가 “<x:y>가 몇 번째 해인지”를 찾을 때, 연도 T를 1부터 올려가며(혹은 x부터 시작해 M씩 증가시키며) 체크한다.
- 만약 T가 M×N을 넘어갈 때까지도 조건을 만족하는 해를 찾지 못했다면, 그 뒤로는 찾아도 마찬가지이므로 “해당 조건을 만족하는 해는 없다(−1)”라고 판정해도 된다.
- 즉, M×N “더 이상 찾아봤자 의미가 없는 안전한 상한”으로 쓰는 것이다.
'백준 문제 풀이' 카테고리의 다른 글
| [백준 / 파이썬] 백준 15649번 문제 풀이: N과 M (1) (0) | 2025.01.29 |
|---|---|
| [백준 / 파이썬] 백준 1748번 문제 풀이: 수 이어 쓰기 1 (0) | 2025.01.16 |
| [백준 / 파이썬] 백준 1107번 문제 풀이: 브루트 포스 (Brute Force) (0) | 2024.09.16 |
| [백준 / 파이썬] 백준 1476번 문제 풀이: 브루트 포스 (Brute Force) (1) | 2024.09.15 |
| [백준 / 파이썬] 백준 3085번 문제 풀이: 브루트 포스 (Brute Force) (0) | 2024.09.14 |